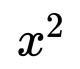Solve x-120500/x=0.02

$$\frac{ x-120500 }{ x } = 0.02$$

Solve for x

$$x = \frac{6025000}{49} = 122959\frac{9}{49} \approx 122959.183673469$$

Steps for Solving Linear Equation

Variable x cannot be equal to 0 since division by zero is not defined. Multiply both sides of the equation by x.

$$x-120500=0.02x$$

Subtract 0.02x from both sides.

$$x-120500-0.02x=0$$

Combine x and -0.02x to get 0.98x.

$$0.98x-120500=0$$

Add 120500 to both sides. Anything plus zero gives itself.

$$0.98x=120500$$

Divide both sides by 0.98.

$$x=\frac{120500}{0.98}$$

Expand \frac{120500}{0.98} by multiplying both numerator and the denominator by 100.

$$x=\frac{12050000}{98}$$

Reduce the fraction \frac{12050000}{98} to lowest terms by extracting and canceling out 2.

$$x=\frac{6025000}{49}$$