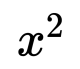{l}{x=y+2z}{3x-z=7}{3z-y=7}-ஐ தீர்க்கவும்

$$\left\{ \begin{array} { l } { x = y + 2z } \\ { 3 x - z = 7 } \\ { 3 z - y = 7 } \end{array} \right.$$

x, y, z-க்காகத் தீர்க்கவும்

$$x=3$$

$$y=-1$$

$$z=2$$

மாற்றைப் பயன்படுத்துகின்ற சிறிய படிகள்

சமன்பாடு 3x-z=7-இல் x-க்கு y+2z-ஐ பதிலிடவும்.

$$3\left(y+2z\right)-z=7$$

y-க்காக இரண்டாவது சமன்பாட்டையும், z-க்காக மூன்றாவது சமன்பாட்டையும் தீர்க்கவும்.

$$y=\frac{7}{3}-\frac{5}{3}z z=\frac{7}{3}+\frac{1}{3}y$$

சமன்பாடு z=\frac{7}{3}+\frac{1}{3}y-இல் y-க்கு \frac{7}{3}-\frac{5}{3}z-ஐ பதிலிடவும்.

$$z=\frac{7}{3}+\frac{1}{3}\left(\frac{7}{3}-\frac{5}{3}z\right)$$

z-க்காக z=\frac{7}{3}+\frac{1}{3}\left(\frac{7}{3}-\frac{5}{3}z\right)-ஐத் தீர்க்கவும்.

$$z=2$$

சமன்பாடு y=\frac{7}{3}-\frac{5}{3}z-இல் z-க்கு 2-ஐ பதிலிடவும்.

$$y=\frac{7}{3}-\frac{5}{3}\times 2$$

y=\frac{7}{3}-\frac{5}{3}\times 2 இலிருந்து y-ஐக் கணக்கிடவும்.

$$y=-1$$

சமன்பாடு x=y+2z-இல் y-க்கு -1-ஐ மற்றும் z-க்கு 2-ஐ பதிலிடவும்.

$$x=-1+2\times 2$$

x=-1+2\times 2 இலிருந்து x-ஐக் கணக்கிடவும்.

$$x=3$$

இப்போது அமைப்பு சரிசெய்யப்பட்டது.

$$x=3 y=-1 z=2$$