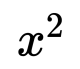Kiértékelés
\left(\begin{matrix}1&3&21\\6&4&35\end{matrix}\right)
Mátrix transzponálása
\left(\begin{matrix}1&6\\3&4\\21&35\end{matrix}\right)
Megosztás
Átmásolva a vágólapra
\left(\begin{matrix}2&3\\5&4\end{matrix}\right)\left(\begin{matrix}2&0&3\\-1&1&5\end{matrix}\right)
A mátrixszorzás akkor van definiálva, ha az első mátrix oszlopainak száma megegyezik a második mátrix sorainak számával.
\left(\begin{matrix}2\times 2+3\left(-1\right)&&\\&&\end{matrix}\right)
Az első mátrix első sorának minden elemét megszorozzuk a második mátrix első oszlopának a megfelelő elemeivel, majd ezeket a szorzatokat összeadva kapjuk meg a szorzatmátrix első sorának első oszlopában lévő elemet.
\left(\begin{matrix}2\times 2+3\left(-1\right)&3&2\times 3+3\times 5\\5\times 2+4\left(-1\right)&4&5\times 3+4\times 5\end{matrix}\right)
Hasonlóképpen kapjuk meg a szorzatmátrix többi elemét.
\left(\begin{matrix}4-3&3&6+15\\10-4&4&15+20\end{matrix}\right)
Az egyes elemeket egyszerűbb alakra hozzuk a tagok szorzásainak elvégzésével.
\left(\begin{matrix}1&3&21\\6&4&35\end{matrix}\right)
Kiszámoljuk a mátrix egyes elemeinek összegét.
Példák
Másodfokú egyenlet
{ x } ^ { 2 } - 4 x - 5 = 0
Trigonometria
4 \sin \theta \cos \theta = 2 \sin \theta
Lineáris egyenlet
y = 3x + 4
Számtan
699 * 533
Mátrix
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{array} \right]
Egyenletrendszer
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right.
Differenciálszámítás
\frac { d } { d x } \frac { ( 3 x ^ { 2 } - 2 ) } { ( x - 5 ) }
Integrálás
\int _ { 0 } ^ { 1 } x e ^ { - x ^ { 2 } } d x
Határértékek
\lim _{x \rightarrow-3} \frac{x^{2}-9}{x^{2}+2 x-3}