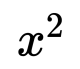Resolver para x
x>-\frac{213}{5}
Gráfico
Compartir
Copiado en el Portapapeles
\frac{52.5+x}{48+50+48+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Suma 28 y 24.5 para obtener 52.5.
\frac{52.5+x}{98+48+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Suma 48 y 50 para obtener 98.
\frac{52.5+x}{146+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Suma 98 y 48 para obtener 146.
\frac{52.5+x}{198}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5
Suma 146 y 52 para obtener 198.
\frac{52.5+x}{198}\times 0.1+\frac{4}{5}\times 0.15+\frac{15}{30}\times 0.75>0.5
Reduzca la fracción \frac{8}{10} a su mínima expresión extrayendo y anulando 2.
\frac{52.5+x}{198}\times 0.1+\frac{4}{5}\times \frac{3}{20}+\frac{15}{30}\times 0.75>0.5
Convierte el número decimal 0.15 a la fracción \frac{15}{100}. Reduzca la fracción \frac{15}{100} a su mínima expresión extrayendo y anulando 5.
\frac{52.5+x}{198}\times 0.1+\frac{4\times 3}{5\times 20}+\frac{15}{30}\times 0.75>0.5
Multiplica \frac{4}{5} por \frac{3}{20} (para hacerlo, multiplica el numerador por el numerador y el denominador por el denominador).
\frac{52.5+x}{198}\times 0.1+\frac{12}{100}+\frac{15}{30}\times 0.75>0.5
Realiza las multiplicaciones en la fracción \frac{4\times 3}{5\times 20}.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{15}{30}\times 0.75>0.5
Reduzca la fracción \frac{12}{100} a su mínima expresión extrayendo y anulando 4.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1}{2}\times 0.75>0.5
Reduzca la fracción \frac{15}{30} a su mínima expresión extrayendo y anulando 15.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1}{2}\times \frac{3}{4}>0.5
Convierte el número decimal 0.75 a la fracción \frac{75}{100}. Reduzca la fracción \frac{75}{100} a su mínima expresión extrayendo y anulando 25.
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1\times 3}{2\times 4}>0.5
Multiplica \frac{1}{2} por \frac{3}{4} (para hacerlo, multiplica el numerador por el numerador y el denominador por el denominador).
\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{3}{8}>0.5
Realiza las multiplicaciones en la fracción \frac{1\times 3}{2\times 4}.
\frac{52.5+x}{198}\times 0.1+\frac{24}{200}+\frac{75}{200}>0.5
El mínimo común múltiplo de 25 y 8 es 200. Convertir \frac{3}{25} y \frac{3}{8} a fracciones con denominador 200.
\frac{52.5+x}{198}\times 0.1+\frac{24+75}{200}>0.5
Como \frac{24}{200} y \frac{75}{200} tienen el mismo denominador, sume sus numeradores para sumarlos.
\frac{52.5+x}{198}\times 0.1+\frac{99}{200}>0.5
Suma 24 y 75 para obtener 99.
\left(\frac{35}{132}+\frac{1}{198}x\right)\times 0.1+\frac{99}{200}>0.5
Divida cada término de 52.5+x entre 198 para obtener \frac{35}{132}+\frac{1}{198}x.
\frac{7}{264}+\frac{1}{198}x\times 0.1+\frac{99}{200}>0.5
Usa la propiedad distributiva para multiplicar \frac{35}{132}+\frac{1}{198}x por 0.1.
\frac{7}{264}+\frac{1}{198}x\times \frac{1}{10}+\frac{99}{200}>0.5
Convierte el número decimal 0.1 a la fracción \frac{1}{10}.
\frac{7}{264}+\frac{1\times 1}{198\times 10}x+\frac{99}{200}>0.5
Multiplica \frac{1}{198} por \frac{1}{10} (para hacerlo, multiplica el numerador por el numerador y el denominador por el denominador).
\frac{7}{264}+\frac{1}{1980}x+\frac{99}{200}>0.5
Realiza las multiplicaciones en la fracción \frac{1\times 1}{198\times 10}.
\frac{175}{6600}+\frac{1}{1980}x+\frac{3267}{6600}>0.5
El mínimo común múltiplo de 264 y 200 es 6600. Convertir \frac{7}{264} y \frac{99}{200} a fracciones con denominador 6600.
\frac{175+3267}{6600}+\frac{1}{1980}x>0.5
Como \frac{175}{6600} y \frac{3267}{6600} tienen el mismo denominador, sume sus numeradores para sumarlos.
\frac{3442}{6600}+\frac{1}{1980}x>0.5
Suma 175 y 3267 para obtener 3442.
\frac{1721}{3300}+\frac{1}{1980}x>0.5
Reduzca la fracción \frac{3442}{6600} a su mínima expresión extrayendo y anulando 2.
\frac{1}{1980}x>0.5-\frac{1721}{3300}
Resta \frac{1721}{3300} en los dos lados.
\frac{1}{1980}x>\frac{1}{2}-\frac{1721}{3300}
Convierte el número decimal 0.5 a la fracción \frac{5}{10}. Reduzca la fracción \frac{5}{10} a su mínima expresión extrayendo y anulando 5.
\frac{1}{1980}x>\frac{1650}{3300}-\frac{1721}{3300}
El mínimo común múltiplo de 2 y 3300 es 3300. Convertir \frac{1}{2} y \frac{1721}{3300} a fracciones con denominador 3300.
\frac{1}{1980}x>\frac{1650-1721}{3300}
Como \frac{1650}{3300} y \frac{1721}{3300} tienen el mismo denominador, reste sus numeradores para restarlos.
\frac{1}{1980}x>-\frac{71}{3300}
Resta 1721 de 1650 para obtener -71.
x>-\frac{71}{3300}\times 1980
Multiplica los dos lados por 1980, el recíproco de \frac{1}{1980}. Dado que \frac{1}{1980} es >0, la dirección de desigualdad sigue siendo la misma.
x>\frac{-71\times 1980}{3300}
Expresa -\frac{71}{3300}\times 1980 como una única fracción.
x>\frac{-140580}{3300}
Multiplica -71 y 1980 para obtener -140580.
x>-\frac{213}{5}
Reduzca la fracción \frac{-140580}{3300} a su mínima expresión extrayendo y anulando 660.
Ejemplos
Ecuación cuadrática
{ x } ^ { 2 } - 4 x - 5 = 0
Trigonometría
4 \sin \theta \cos \theta = 2 \sin \theta
Ecuación lineal
y = 3x + 4
Aritmética
699 * 533
Matriz
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{array} \right]
Ecuación simultánea
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right.
Diferenciación
\frac { d } { d x } \frac { ( 3 x ^ { 2 } - 2 ) } { ( x - 5 ) }
Integración
\int _ { 0 } ^ { 1 } x e ^ { - x ^ { 2 } } d x
Límites
\lim _{x \rightarrow-3} \frac{x^{2}-9}{x^{2}+2 x-3}