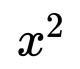Solve 2x^2-x-3=0

$$2 { x }^{ 2 } -x-3 = 0$$

Solve for x

$$x=-1$$

$$x = \frac{3}{2} = 1\frac{1}{2} = 1.5$$

Steps Using Factoring By Grouping

To solve the equation, factor the left hand side by grouping. First, left hand side needs to be rewritten as 2x^{2}+ax+bx-3. To find a and b, set up a system to be solved.

$$a+b=-1 ab=2\left(-3\right)=-6$$

Since ab is negative, a and b have the opposite signs. Since a+b is negative, the negative number has greater absolute value than the positive. List all such integer pairs that give product -6.

$$1,-6 2,-3$$

Calculate the sum for each pair.

$$1-6=-5 2-3=-1$$

The solution is the pair that gives sum -1.

$$a=-3 b=2$$

Rewrite 2x^{2}-x-3 as \left(2x^{2}-3x\right)+\left(2x-3\right).

$$\left(2x^{2}-3x\right)+\left(2x-3\right)$$

Factor out x in 2x^{2}-3x.

$$x\left(2x-3\right)+2x-3$$

Factor out common term 2x-3 by using distributive property.

$$\left(2x-3\right)\left(x+1\right)$$

To find equation solutions, solve 2x-3=0 and x+1=0.

$$x=\frac{3}{2} x=-1$$

Steps Using the Quadratic Formula

All equations of the form ax^{2}+bx+c=0 can be solved using the quadratic formula: \frac{-b±\sqrt{b^{2}-4ac}}{2a}. The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.

$$2x^{2}-x-3=0$$

This equation is in standard form: ax^{2}+bx+c=0. Substitute 2 for a, -1 for b, and -3 for c in the quadratic formula, \frac{-b±\sqrt{b^{2}-4ac}}{2a}.

$$x=\frac{-\left(-1\right)±\sqrt{1-4\times 2\left(-3\right)}}{2\times 2}$$

Multiply -4 times 2.

$$x=\frac{-\left(-1\right)±\sqrt{1-8\left(-3\right)}}{2\times 2}$$

Multiply -8 times -3.

$$x=\frac{-\left(-1\right)±\sqrt{1+24}}{2\times 2}$$

Add 1 to 24.

$$x=\frac{-\left(-1\right)±\sqrt{25}}{2\times 2}$$

Take the square root of 25.

$$x=\frac{-\left(-1\right)±5}{2\times 2}$$

The opposite of -1 is 1.

$$x=\frac{1±5}{2\times 2}$$

Multiply 2 times 2.

$$x=\frac{1±5}{4}$$

Now solve the equation x=\frac{1±5}{4} when ± is plus. Add 1 to 5.

$$x=\frac{6}{4}$$

Reduce the fraction \frac{6}{4} to lowest terms by extracting and canceling out 2.

$$x=\frac{3}{2}$$

Now solve the equation x=\frac{1±5}{4} when ± is minus. Subtract 5 from 1.

$$x=-\frac{4}{4}$$

Divide -4 by 4.

$$x=-1$$

The equation is now solved.

$$x=\frac{3}{2} x=-1$$

Steps for Completing the Square

Quadratic equations such as this one can be solved by completing the square. In order to complete the square, the equation must first be in the form x^{2}+bx=c.

$$2x^{2}-x-3=0$$

Add 3 to both sides of the equation.

$$2x^{2}-x-3-\left(-3\right)=-\left(-3\right)$$

Subtracting -3 from itself leaves 0.

$$2x^{2}-x=-\left(-3\right)$$

Subtract -3 from 0.

$$2x^{2}-x=3$$

Divide both sides by 2.

$$\frac{2x^{2}-x}{2}=\frac{3}{2}$$

Dividing by 2 undoes the multiplication by 2.

$$x^{2}-\frac{1}{2}x=\frac{3}{2}$$

Divide -\frac{1}{2}, the coefficient of the x term, by 2 to get -\frac{1}{4}. Then add the square of -\frac{1}{4} to both sides of the equation. This step makes the left hand side of the equation a perfect square.

$$x^{2}-\frac{1}{2}x+\left(-\frac{1}{4}\right)^{2}=\frac{3}{2}+\left(-\frac{1}{4}\right)^{2}$$

Square -\frac{1}{4} by squaring both the numerator and the denominator of the fraction.

$$x^{2}-\frac{1}{2}x+\frac{1}{16}=\frac{3}{2}+\frac{1}{16}$$

Add \frac{3}{2} to \frac{1}{16} by finding a common denominator and adding the numerators. Then reduce the fraction to lowest terms if possible.

$$x^{2}-\frac{1}{2}x+\frac{1}{16}=\frac{25}{16}$$

Factor x^{2}-\frac{1}{2}x+\frac{1}{16}. In general, when x^{2}+bx+c is a perfect square, it can always be factored as \left(x+\frac{b}{2}\right)^{2}.

$$\left(x-\frac{1}{4}\right)^{2}=\frac{25}{16}$$

Take the square root of both sides of the equation.

$$\sqrt{\left(x-\frac{1}{4}\right)^{2}}=\sqrt{\frac{25}{16}}$$

Simplify.

$$x-\frac{1}{4}=\frac{5}{4} x-\frac{1}{4}=-\frac{5}{4}$$

Add \frac{1}{4} to both sides of the equation.

$$x=\frac{3}{2} x=-1$$