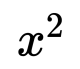Solve for x
\left\{\begin{matrix}\\x=z\text{, }&\text{unconditionally}\\x\in \mathrm{R}\text{, }&y=0\end{matrix}\right.
Solve for y
\left\{\begin{matrix}\\y=0\text{, }&\text{unconditionally}\\y\in \mathrm{R}\text{, }&x=z\end{matrix}\right.
Share
Copied to clipboard
xz+yz=zx+yx
Use the distributive property to multiply x+y by z.
xz+yz-zx=yx
Subtract zx from both sides.
yz=yx
Combine xz and -zx to get 0.
yx=yz
Swap sides so that all variable terms are on the left hand side.
\frac{yx}{y}=\frac{yz}{y}
Divide both sides by y.
x=\frac{yz}{y}
Dividing by y undoes the multiplication by y.
x=z
Divide yz by y.
xz+yz=zx+yx
Use the distributive property to multiply x+y by z.
xz+yz-yx=zx
Subtract yx from both sides.
yz-yx=zx-xz
Subtract xz from both sides.
yz-yx=0
Combine zx and -xz to get 0.
\left(z-x\right)y=0
Combine all terms containing y.
y=0
Divide 0 by -x+z.
Examples
Quadratic equation
{ x } ^ { 2 } - 4 x - 5 = 0
Trigonometry
4 \sin \theta \cos \theta = 2 \sin \theta
Linear equation
y = 3x + 4
Arithmetic
699 * 533
Matrix
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{array} \right]
Simultaneous equation
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right.
Differentiation
\frac { d } { d x } \frac { ( 3 x ^ { 2 } - 2 ) } { ( x - 5 ) }
Integration
\int _ { 0 } ^ { 1 } x e ^ { - x ^ { 2 } } d x
Limits
\lim _{x \rightarrow-3} \frac{x^{2}-9}{x^{2}+2 x-3}