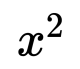Solve x^2-5x+4=0

$${ x }^{ 2 } -5x+4=0$$

Solve for x

$$x=1$$

$$x=4$$

Steps Using Factoring

To solve the equation, factor x^{2}-5x+4 using formula x^{2}+\left(a+b\right)x+ab=\left(x+a\right)\left(x+b\right). To find a and b, set up a system to be solved.

$$a+b=-5 ab=4$$

Since ab is positive, a and b have the same sign. Since a+b is negative, a and b are both negative. List all such integer pairs that give product 4.

$$-1,-4 -2,-2$$

Calculate the sum for each pair.

$$-1-4=-5 -2-2=-4$$

The solution is the pair that gives sum -5.

$$a=-4 b=-1$$

Rewrite factored expression \left(x+a\right)\left(x+b\right) using the obtained values.

$$\left(x-4\right)\left(x-1\right)$$

To find equation solutions, solve x-4=0 and x-1=0.

$$x=4 x=1$$

Steps Using Factoring By Grouping

To solve the equation, factor the left hand side by grouping. First, left hand side needs to be rewritten as x^{2}+ax+bx+4. To find a and b, set up a system to be solved.

$$a+b=-5 ab=1\times 4=4$$

Since ab is positive, a and b have the same sign. Since a+b is negative, a and b are both negative. List all such integer pairs that give product 4.

$$-1,-4 -2,-2$$

Calculate the sum for each pair.

$$-1-4=-5 -2-2=-4$$

The solution is the pair that gives sum -5.

$$a=-4 b=-1$$

Rewrite x^{2}-5x+4 as \left(x^{2}-4x\right)+\left(-x+4\right).

$$\left(x^{2}-4x\right)+\left(-x+4\right)$$

Factor out x in the first and -1 in the second group.

$$x\left(x-4\right)-\left(x-4\right)$$

Factor out common term x-4 by using distributive property.

$$\left(x-4\right)\left(x-1\right)$$

To find equation solutions, solve x-4=0 and x-1=0.

$$x=4 x=1$$

Steps Using the Quadratic Formula

All equations of the form ax^{2}+bx+c=0 can be solved using the quadratic formula: \frac{-b±\sqrt{b^{2}-4ac}}{2a}. The quadratic formula gives two solutions, one when ± is addition and one when it is subtraction.

$$x^{2}-5x+4=0$$

This equation is in standard form: ax^{2}+bx+c=0. Substitute 1 for a, -5 for b, and 4 for c in the quadratic formula, \frac{-b±\sqrt{b^{2}-4ac}}{2a}.

$$x=\frac{-\left(-5\right)±\sqrt{\left(-5\right)^{2}-4\times 4}}{2}$$

Square -5.

$$x=\frac{-\left(-5\right)±\sqrt{25-4\times 4}}{2}$$

Multiply -4 times 4.

$$x=\frac{-\left(-5\right)±\sqrt{25-16}}{2}$$

Add 25 to -16.

$$x=\frac{-\left(-5\right)±\sqrt{9}}{2}$$

Take the square root of 9.

$$x=\frac{-\left(-5\right)±3}{2}$$

The opposite of -5 is 5.

$$x=\frac{5±3}{2}$$

Now solve the equation x=\frac{5±3}{2} when ± is plus. Add 5 to 3.

$$x=\frac{8}{2}$$

Divide 8 by 2.

$$x=4$$

Now solve the equation x=\frac{5±3}{2} when ± is minus. Subtract 3 from 5.

$$x=\frac{2}{2}$$

Divide 2 by 2.

$$x=1$$

The equation is now solved.

$$x=4 x=1$$

Steps for Completing the Square

Quadratic equations such as this one can be solved by completing the square. In order to complete the square, the equation must first be in the form x^{2}+bx=c.

$$x^{2}-5x+4=0$$

Subtract 4 from both sides of the equation.

$$x^{2}-5x+4-4=-4$$

Subtracting 4 from itself leaves 0.

$$x^{2}-5x=-4$$

Divide -5, the coefficient of the x term, by 2 to get -\frac{5}{2}. Then add the square of -\frac{5}{2} to both sides of the equation. This step makes the left hand side of the equation a perfect square.

$$x^{2}-5x+\left(-\frac{5}{2}\right)^{2}=-4+\left(-\frac{5}{2}\right)^{2}$$

Square -\frac{5}{2} by squaring both the numerator and the denominator of the fraction.

$$x^{2}-5x+\frac{25}{4}=-4+\frac{25}{4}$$

Add -4 to \frac{25}{4}.

$$x^{2}-5x+\frac{25}{4}=\frac{9}{4}$$

Factor x^{2}-5x+\frac{25}{4}. In general, when x^{2}+bx+c is a perfect square, it can always be factored as \left(x+\frac{b}{2}\right)^{2}.

$$\left(x-\frac{5}{2}\right)^{2}=\frac{9}{4}$$

Take the square root of both sides of the equation.

$$\sqrt{\left(x-\frac{5}{2}\right)^{2}}=\sqrt{\frac{9}{4}}$$

Simplify.

$$x-\frac{5}{2}=\frac{3}{2} x-\frac{5}{2}=-\frac{3}{2}$$

Add \frac{5}{2} to both sides of the equation.

$$x=4 x=1$$