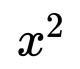Evaluate
\left(\begin{matrix}1&3&21\\6&4&35\end{matrix}\right)
Transpose Matrix
\left(\begin{matrix}1&6\\3&4\\21&35\end{matrix}\right)
Share
Copied to clipboard
\left(\begin{matrix}2&3\\5&4\end{matrix}\right)\left(\begin{matrix}2&0&3\\-1&1&5\end{matrix}\right)
Matrix multiplication is defined if the number of columns of the first matrix is equal to the number of rows of the second matrix.
\left(\begin{matrix}2\times 2+3\left(-1\right)&&\\&&\end{matrix}\right)
Multiply each element of the first row of the first matrix by the corresponding element of the first column of the second matrix and then add these products to obtain the element in the first row, first column of the product matrix.
\left(\begin{matrix}2\times 2+3\left(-1\right)&3&2\times 3+3\times 5\\5\times 2+4\left(-1\right)&4&5\times 3+4\times 5\end{matrix}\right)
The remaining elements of the product matrix are found in the same way.
\left(\begin{matrix}4-3&3&6+15\\10-4&4&15+20\end{matrix}\right)
Simplify each element by multiplying the individual terms.
\left(\begin{matrix}1&3&21\\6&4&35\end{matrix}\right)
Sum each element of the matrix.
Examples
Quadratic equation
{ x } ^ { 2 } - 4 x - 5 = 0
Trigonometry
4 \sin \theta \cos \theta = 2 \sin \theta
Linear equation
y = 3x + 4
Arithmetic
699 * 533
Matrix
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{array} \right]
Simultaneous equation
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right.
Differentiation
\frac { d } { d x } \frac { ( 3 x ^ { 2 } - 2 ) } { ( x - 5 ) }
Integration
\int _ { 0 } ^ { 1 } x e ^ { - x ^ { 2 } } d x
Limits
\lim _{x \rightarrow-3} \frac{x^{2}-9}{x^{2}+2 x-3}