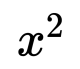\frac { 0,0001 \cdot ( 0,01 ) ^ { 2 } \cdot 1000 } { 0,0001 }
Evaluate
0,1
Factor
\frac{1}{2 \cdot 5} = 0.1
Share
Copied to clipboard
0,01^{2}\times 1000
Cancel out 0,0001 and 0,0001.
0,0001\times 1000
Calculate 0,01 to the power of 2 and get 0,0001.
0,1
Multiply 0,0001 and 1000 to get 0,1.
Examples
Quadratic equation
{ x } ^ { 2 } - 4 x - 5 = 0
Trigonometry
4 \sin \theta \cos \theta = 2 \sin \theta
Linear equation
y = 3x + 4
Arithmetic
699 * 533
Matrix
\left[ \begin{array} { l l } { 2 } & { 3 } \\ { 5 } & { 4 } \end{array} \right] \left[ \begin{array} { l l l } { 2 } & { 0 } & { 3 } \\ { -1 } & { 1 } & { 5 } \end{array} \right]
Simultaneous equation
\left. \begin{cases} { 8x+2y = 46 } \\ { 7x+3y = 47 } \end{cases} \right.
Differentiation
\frac { d } { d x } \frac { ( 3 x ^ { 2 } - 2 ) } { ( x - 5 ) }
Integration
\int _ { 0 } ^ { 1 } x e ^ { - x ^ { 2 } } d x
Limits
\lim _{x \rightarrow-3} \frac{x^{2}-9}{x^{2}+2 x-3}