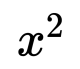Επίλυση (28+24.5+x/48+50+48+52)*0.1+8/10*0.15+15/30*0.75>0.5

$$( \frac{ 28+24.5+x }{ 48+50+48+52 } ) \times 0.1+ \frac{ 8 }{ 10 } \times 0.15+ \frac{ 15 }{ 30 } \times 0.75 > 0.5$$

Λύση ως προς x

$$x>-\frac{213}{5}$$

Βήματα λύσης

Προσθέστε 28 και 24.5 για να λάβετε 52.5.

$$\frac{52.5+x}{48+50+48+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5$$

Προσθέστε 48 και 50 για να λάβετε 98.

$$\frac{52.5+x}{98+48+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5$$

Προσθέστε 98 και 48 για να λάβετε 146.

$$\frac{52.5+x}{146+52}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5$$

Προσθέστε 146 και 52 για να λάβετε 198.

$$\frac{52.5+x}{198}\times 0.1+\frac{8}{10}\times 0.15+\frac{15}{30}\times 0.75>0.5$$

Μειώστε το κλάσμα \frac{8}{10} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 2.

$$\frac{52.5+x}{198}\times 0.1+\frac{4}{5}\times 0.15+\frac{15}{30}\times 0.75>0.5$$

Μετατροπή του δεκαδικού αριθμού 0.15 στο κλάσμα \frac{15}{100}. Μειώστε το κλάσμα \frac{15}{100} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 5.

$$\frac{52.5+x}{198}\times 0.1+\frac{4}{5}\times \frac{3}{20}+\frac{15}{30}\times 0.75>0.5$$

Πολλαπλασιάστε το \frac{4}{5} επί \frac{3}{20} πολλαπλασιάζοντας τον αριθμητή επί τον αριθμητή και τον παρονομαστή επί τον παρονομαστή.

$$\frac{52.5+x}{198}\times 0.1+\frac{4\times 3}{5\times 20}+\frac{15}{30}\times 0.75>0.5$$

Κάντε τους πολλαπλασιασμούς στο κλάσμα \frac{4\times 3}{5\times 20}.

$$\frac{52.5+x}{198}\times 0.1+\frac{12}{100}+\frac{15}{30}\times 0.75>0.5$$

Μειώστε το κλάσμα \frac{12}{100} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 4.

$$\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{15}{30}\times 0.75>0.5$$

Μειώστε το κλάσμα \frac{15}{30} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 15.

$$\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1}{2}\times 0.75>0.5$$

Μετατροπή του δεκαδικού αριθμού 0.75 στο κλάσμα \frac{75}{100}. Μειώστε το κλάσμα \frac{75}{100} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 25.

$$\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1}{2}\times \frac{3}{4}>0.5$$

Πολλαπλασιάστε το \frac{1}{2} επί \frac{3}{4} πολλαπλασιάζοντας τον αριθμητή επί τον αριθμητή και τον παρονομαστή επί τον παρονομαστή.

$$\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{1\times 3}{2\times 4}>0.5$$

Κάντε τους πολλαπλασιασμούς στο κλάσμα \frac{1\times 3}{2\times 4}.

$$\frac{52.5+x}{198}\times 0.1+\frac{3}{25}+\frac{3}{8}>0.5$$

Το ελάχιστο κοινό πολλαπλάσιο των 25 και 8 είναι 200. Μετατροπή των \frac{3}{25} και \frac{3}{8} σε κλάσματα με παρονομαστή 200.

$$\frac{52.5+x}{198}\times 0.1+\frac{24}{200}+\frac{75}{200}>0.5$$

Από τη στιγμή που οι αριθμοί \frac{24}{200} και \frac{75}{200} έχουν τον ίδιο παρονομαστή, μπορείτε να τους προσθέσετε προσθέτοντας τους αριθμητές τους.

$$\frac{52.5+x}{198}\times 0.1+\frac{24+75}{200}>0.5$$

Προσθέστε 24 και 75 για να λάβετε 99.

$$\frac{52.5+x}{198}\times 0.1+\frac{99}{200}>0.5$$

Διαιρέστε κάθε όρο του 52.5+x με το 198 για να λάβετε \frac{35}{132}+\frac{1}{198}x.

$$\left(\frac{35}{132}+\frac{1}{198}x\right)\times 0.1+\frac{99}{200}>0.5$$

Χρησιμοποιήστε την επιμεριστική ιδιότητα για να πολλαπλασιάσετε το \frac{35}{132}+\frac{1}{198}x με το 0.1.

$$\frac{7}{264}+\frac{1}{198}x\times 0.1+\frac{99}{200}>0.5$$

Μετατροπή του δεκαδικού αριθμού 0.1 στο κλάσμα \frac{1}{10}.

$$\frac{7}{264}+\frac{1}{198}x\times \frac{1}{10}+\frac{99}{200}>0.5$$

Πολλαπλασιάστε το \frac{1}{198} επί \frac{1}{10} πολλαπλασιάζοντας τον αριθμητή επί τον αριθμητή και τον παρονομαστή επί τον παρονομαστή.

$$\frac{7}{264}+\frac{1\times 1}{198\times 10}x+\frac{99}{200}>0.5$$

Κάντε τους πολλαπλασιασμούς στο κλάσμα \frac{1\times 1}{198\times 10}.

$$\frac{7}{264}+\frac{1}{1980}x+\frac{99}{200}>0.5$$

Το ελάχιστο κοινό πολλαπλάσιο των 264 και 200 είναι 6600. Μετατροπή των \frac{7}{264} και \frac{99}{200} σε κλάσματα με παρονομαστή 6600.

$$\frac{175}{6600}+\frac{1}{1980}x+\frac{3267}{6600}>0.5$$

Από τη στιγμή που οι αριθμοί \frac{175}{6600} και \frac{3267}{6600} έχουν τον ίδιο παρονομαστή, μπορείτε να τους προσθέσετε προσθέτοντας τους αριθμητές τους.

$$\frac{175+3267}{6600}+\frac{1}{1980}x>0.5$$

Προσθέστε 175 και 3267 για να λάβετε 3442.

$$\frac{3442}{6600}+\frac{1}{1980}x>0.5$$

Μειώστε το κλάσμα \frac{3442}{6600} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 2.

$$\frac{1721}{3300}+\frac{1}{1980}x>0.5$$

Αφαιρέστε \frac{1721}{3300} και από τις δύο πλευρές.

$$\frac{1}{1980}x>0.5-\frac{1721}{3300}$$

Μετατροπή του δεκαδικού αριθμού 0.5 στο κλάσμα \frac{5}{10}. Μειώστε το κλάσμα \frac{5}{10} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 5.

$$\frac{1}{1980}x>\frac{1}{2}-\frac{1721}{3300}$$

Το ελάχιστο κοινό πολλαπλάσιο των 2 και 3300 είναι 3300. Μετατροπή των \frac{1}{2} και \frac{1721}{3300} σε κλάσματα με παρονομαστή 3300.

$$\frac{1}{1980}x>\frac{1650}{3300}-\frac{1721}{3300}$$

Από τη στιγμή που οι αριθμοί \frac{1650}{3300} και \frac{1721}{3300} έχουν τον ίδιο παρονομαστή, μπορείτε να τους αφαιρέσετε αφαιρώντας τους αριθμητές τους.

$$\frac{1}{1980}x>\frac{1650-1721}{3300}$$

Αφαιρέστε 1721 από 1650 για να λάβετε -71.

$$\frac{1}{1980}x>-\frac{71}{3300}$$

Πολλαπλασιάστε και τις δύο πλευρές με 1980, το αντίστροφο του \frac{1}{1980}. Δεδομένου ότι το \frac{1}{1980} είναι >0, η κατεύθυνση της ανισότητας παραμένει η ίδια.

$$x>-\frac{71}{3300}\times 1980$$

Έκφραση του -\frac{71}{3300}\times 1980 ως ενιαίου κλάσματος.

$$x>\frac{-71\times 1980}{3300}$$

Πολλαπλασιάστε -71 και 1980 για να λάβετε -140580.

$$x>\frac{-140580}{3300}$$

Μειώστε το κλάσμα \frac{-140580}{3300} σε χαμηλότερους όρους με την εξαγωγή και την ακύρωση του 660.

$$x>-\frac{213}{5}$$